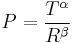Proportionally fair
Proportional fair is a compromise-based scheduling algorithm. It's based upon maintaining a balance between two competing interests: Trying to maximize total wireless network throughput while at the same time allowing all users at least a minimal level of service. This is done by assigning each data flow a data rate or a scheduling priority (depending on the implementation) that is inversely proportional to its anticipated resource consumption.[1]
Contents |
Weighted fair queuing
Proportionally fair scheduling can be achieved by means of weighted fair queuing (WFQ), by setting the scheduling weights for data flow  to
to 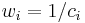 , where the cost
, where the cost 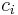 is the amount of consumed resources per data bit. For instance:
is the amount of consumed resources per data bit. For instance:
- In CDMA spread spectrum cellular networks, the cost may be the required energy per bit in the transmit power control (the increased interference level).
- In wireless communication with link adaptation, the cost may be the required time to transmit a certain number of bits using the modulation and error coding scheme that this required. An example of this is EVDO networks, where reported SNR is used as the primary costing factor.
- In wireless networks with fast Dynamic Channel Allocation, the cost may be the number of nearby base station sites that can not use the same frequency channel simultaneously, in view to avoid co-channel interference.
User prioritization
Another way to schedule data transfer that leads to similar results is through the use of prioritization coefficients.[2] Here we schedule the channel for the station that has the maximum of the priority function:
 denotes the data rate potentially achievable for the station in the present time slot.
denotes the data rate potentially achievable for the station in the present time slot. is the historical average data rate of this station.
is the historical average data rate of this station. and
and  tune the "fairness" of the scheduler.
tune the "fairness" of the scheduler.
By adjusting  and
and  in the formula above, we are able to adjust the balance between serving the best mobiles (the ones in the best channel conditions) more often and serving the costly mobiles often enough that they have an acceptable level of performance.
in the formula above, we are able to adjust the balance between serving the best mobiles (the ones in the best channel conditions) more often and serving the costly mobiles often enough that they have an acceptable level of performance.
In the extreme case (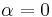 and
and 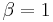 ) the scheduler acts in a round-robin fashion and serves all mobiles equally often, with no regard for resource consumption. If
) the scheduler acts in a round-robin fashion and serves all mobiles equally often, with no regard for resource consumption. If 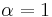 and
and 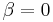 then the scheduler will always serve the mobile with the best channel conditions. This will maximize the throughput of the channel while stations with low
then the scheduler will always serve the mobile with the best channel conditions. This will maximize the throughput of the channel while stations with low  are not served at all. Using
are not served at all. Using 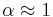 and
and 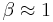 will yield the proportional fair scheduling algorithm used in 3G networks.[2]
will yield the proportional fair scheduling algorithm used in 3G networks.[2]
This technique can be further parametrized by using a "memory constant" that determines the period of time over which the station data rate used in calculating the priority function is averaged. A larger constant generally improves throughput at the expense of reduced short-term fairness.
See also
References
- ^ Kushner, H. J.; Whiting, P.A. (July 2004), "Convergence of proportional-fair sharing algorithms under general conditions", IEEE Transactions on Wireless Communications 3 (4): 1250–1259, doi:10.1109/TWC.2004.830826.
- ^ a b Yang, Ji; Zhang Yifan; Wang Ying; Zhang Ping (2004-11-29), "Average rate updating mechanism in proportional fair scheduler for HDR", IEEE Global Telecommunications Conference, 2004., 6, IEEE, pp. 3464–3466, doi:10.1109/GLOCOM.2004.1379010
Additional reading
- Andrews, Matthew (September 2004), "Instability of the Proportional Fair Scheduling Algorithm for HDR", IEEE Transactions on Wireless Communications 3 (5): 1422–1426, doi:10.1109/TWC.2004.833419.
- Andrews, Matthew; K. Kumaran, K. Ramanan, A. Stoyar and Phil Whitting (February 2001), "Providing Quality of Service over a Shared Wireless Link", IEEE Communications 39 (2): 150–154, doi:10.1109/35.900644.